論文を読んでいると出てくるのが「p<0.05で統計的に有意差があった」という言葉。
例えばカフェインの摂取による筋力向上を調べた研究で「実験前後の筋力差はp<0.05であり、統計的に有意差があった」と書いてあったとする。
ようじゅなんとなくカフェインが効果があったみたいだけど、どんな計算をしているかチンプンカンプン...という人も多いのではないでしょうか
かくいう自分も論文を読み始めた当初は同じだったので、その気持ちは痛いほどわかる。
そこで今回は、論文を読みたい人向けに「統計処理の裏で行われているもの」を解説。
その中でも今回は、２つ以下のグループにおける”差の検定”である”t検定”について、紹介していく。
ようじゅ３つ以上のグループでの差の検定は”分散分析”の記事を参照してください
今回はt検定の難しい数学的理論を学ぶのではなく、t検定の基本的な概念を理解することを目標にする。
ようじゅ自分もt検定と論文にある”統計手法”が繋がらず苦労しました。この記事では数学は最低限に、あくまで(ダイエット・筋トレ)論文の理解を助けることを目的にしました
統計の基本
帰無仮説と対立仮説
ようじゅまずは統計で基本となる"仮説の立て方"について紹介します
統計では、基本的に”帰無仮説”というものを立てる。
ざっくりと言ってしまえば、とりあえず「差がなかった」という仮説のこと。
例えばカフェインの摂取による筋力の向上を調べた研究であれば、「カフェインによる筋力の向上は起こらなかった」という帰無仮説を立てる。
その前提をもとに実験結果の通りになる確率を計算し、その確率が低い場合は帰無仮説を"棄却"する。
ようじゅ棄却するということは、初めに立てた帰無仮説が合っているとは到底思えないと結論づけることです
そして帰無仮説を間違いと判断した（棄却した）ときに成り立つ理論を対立仮説と呼ぶ。
- 帰無仮説「カフェインは筋力を向上させなかった」
- 対立仮説「カフェインは筋力を向上させた」
ようじゅ直接的に「カフェインが筋力を向上させた」とは言わずに、「カフェインが筋力を向上させていないと辻褄があわない」みたいなスタンスを取ります
帰無仮説の前提のもとに実験結果が得られる確率をP値と呼び、その値が5%以下(P<0.05)であれば帰無仮説を棄却して”有意差”ありと結論づける。
ようじゅちなみに”0.05”という数字はロナルド・A・フィッシャーが1925年に発表した論文である『Statistical Methods for Research Workers』で提唱されてから長年続く”慣習”です（R）
全体的な流れを簡単にまとめると「帰無仮説を立てる→P値を計算する→帰無仮説を棄却するか判断する」が大枠になる。
ようじゅP値の解釈は厳密には語弊がありますが、とりあえず論文を読む分にはこれで十分です
「対応のあるt検定」と「対応のないt検定」
t検定における帰無仮説の立て方には、おおまかに分けて２パターンが存在する。
- 被験者内の差を検定する（対応のあるt検定）
- 被験者間の差を検定する（対応のないt検定）
ようじゅどちらも差を0と仮定するのは同じですが、計算がちょっと変わります。ちなみに対応のないt検定のほうが面倒です
対応のないt検定は別名「独立2群のt検定」とも呼ばれる。
ようじゅ論文では実験前後の差を検定するために使われるのが対応のあるt検定。グループ間の差を検定するために使われるのが独立2群のt検定です
対応のあるt検定（Time Effect）
対応のあるt検定の基本
対応のあるt検定ではTime Effectを調べる
ようじゅ対応のあるt検定では、実験前後の値に差があったかを調べるときに使われます
イメージしやすいように具体例を考えてみよう。
例えばあなたが研究者だったとして、カフェインが筋力を上げるかを知りたかったとする。
実際に5人の被験者を集めて実験を行い、ベンチプレスの1RMについて得られたデータは以下のとおり。
| 被験者 | 実験前 | 実験後 | 差d |
|---|---|---|---|
| 被験者１ | 124kg | 148kg | +24kg |
| 被験者２ | 125kg | 138kg | +13kg |
| 被験者３ | 116kg | 132kg | +16kg |
| 被験者４ | 110kg | 107kg | -3kg |
| 被験者５ | 127kg | 142kg | +15kg |
ようじゅあとで使うので実験前後の差も抜き出しておきましょう
このとき知りたいのはカフェインの摂取前後で1RMに差があるか？であり、比較するのは各被験者における1RMの変化。
ようじゅ例えば"被験者Aの実験前1RM"と"被験者Cの実験後1RMを比較することは意味がありません。このように比較する数値が1対1に対応しているので”対応のあるt検定”と呼びます
これらの実験結果を数直線上に表すと下記のようになる。
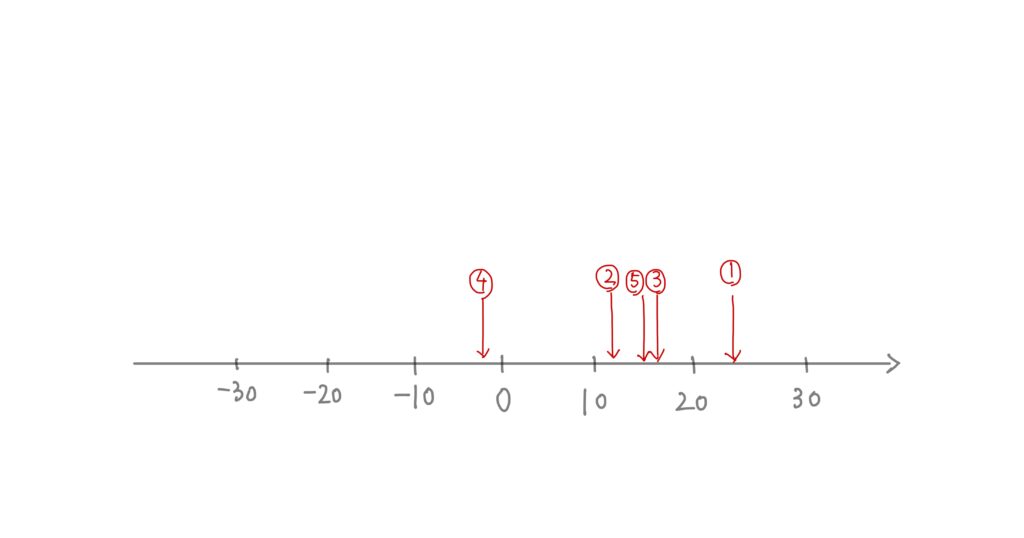
ようじゅ5人中4人はカフェインによって筋力が向上しています。一見効果がありそうなカフェインに対して、実際はどうなのかを調べていくことになります
得られたデータに対する2つの考え
ようじゅここからは"得られた差d"について統計処理をしていきます
この差dのデータがどういった”母集団”から得られた値なのかというのは、2つの立場がある。
- 母平均μdが０の確率分布から得られた
- 母平均μdが０ではない確率分布から得られた
ようじゅ結論を言ってしまえば❶が帰無仮説、❷が対立仮説です
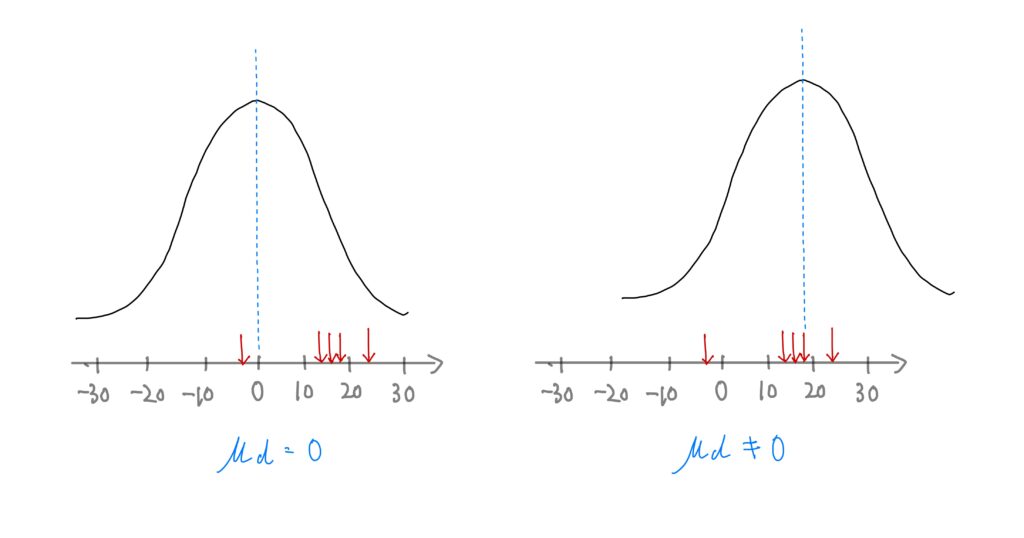
❶は5つの値中４つがプラスの値とはいえ、これは母平均μdが０の確率分布から”偶然”今回のような数値が得られたとする立場。
ようじゅ実験前後の差dは0を中心とした分布で、ばらつきこそあれど基本的には0が中心という考えです
一方で❷の立場は、母平均μdが０ではないと考える立場。
実験前後の差dは、0ではないプラスを中心に分布していると考える。
この❶と❷がこのt検定における帰無仮説と対立仮説になる。
- 帰無仮説「実験前後で差はない（μ=０）」
- 対立仮説「実験前後で差がある（μ≠０）」
ようじゅここからの検定では帰無仮説を前提に計算をすすめ、その前提のもとで今回の実験結果は本当に起こりえるか？を考えます
対応のあるt検定、その全体像
最終目標は得られた差の平均が従う確率分布を標準正規分布にすること
まず最初に全体像を紹介しておこう。
まずt検定における最終到達点は、差dの平均$\overline{d}$が従う確率分布を"標準正規分布"というものに直すこと。
ようじゅここでいう標準正規分布とは平均0、標準偏差が１の分布です
最終的に見るべきは各被験者の差dの平均値である$\overline{d}$なので、この分布について考えるのは理解しやすいはず。
そしてなぜこの分布を標準正規分布にしたいかというと、標準正規分布は過去に数学者が調べ尽くしており、得られた実験値($\overline{d}$)がどれくらいの確率で得られるかがわかるからである。
ようじゅそしてこの確率が低いならば帰無仮説を棄却できる...ということになります
しかし実際には正規化に必要なデータがわからないので、得られるデータから"正規化もどき"をすることになる。
ようじゅこうして求められるのが標準正規分布に近いt分布と呼ばれるものです
そして「正規化もどきをしたt分布から今回の実験結果がどれくらい得られそうか？」を考えるのがt検定の全体像になる。